Ovals and various "egg shaped" designs are often used in marquetry, especially for such purposes as framing marquetry portraits in a similar manner to the ovals cut in mount board as done by photographers. But, you may ask, how do I actually draw out such a design in the first place? Well, never fear, because I am about to guide you through the process of drawing all manner of such designs. So, are you ready? right then, off we go:

I am now going to describe to you a few of the alternative methods used for the construction of an ellipse and various ovals. No part of an ellipse is an arc, which is part of a circle, and so a true ellipse cannot be drawn with a compass. I have always used the trammel method described by Eddie Stevens in Journal No. 219.

I thought the string method too big and clumsy for marquetry purposes, and more suitable for setting out flower beds. However, on trying it I found that it was not difficult to get a good result.

Here is the method: -

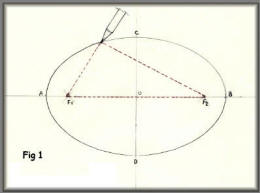
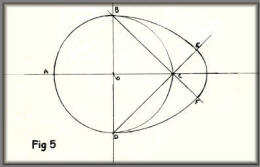
Draw the long and short centrelines, crossing at 0 and mark the extremities A,B,C, and D, Open the compass to AO and with point on D, draw arcs to cut line AB at points F¹ and F², called the focal points. Make a "string loop" - I used button thread; with length from F¹ to B. I found the easiest way to do this was to cut a piece of veneer, say about 1 inch wide, length F¹ to B and tie the loop around it. Put a small nail or suitable pin (I used a drawing pin which could be pushed through from behind) at each focal point, and now use the loop as shown in the sketch - using a sharp pencil to describe the circumference of the ellipse.

By ellipse we mean a true ellipse as obtained by the trammel method. By oval, we mean a near or approximation drawn with a compass.

The method of construction of an oval (which in my experience has been the most common) is as follows;­

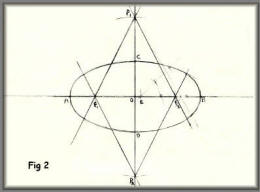
Draw a line A B (Fig 2) equal in length to the long diameter of the oval, and through the middle point O of this diameter draw a line at right angles. Make O C and O D each equal to half the small diameter of the oval. From A mark off A E equal in length to C D. Divide E B into three equal parts. Now set the compasses at a radius equal to two of the parts, and with O as centre, mark points F1, F2. Then with O again as centre, and the compasses set to length F1 (F2), mark points P1, (P2). It will be seen that either O P is equal to four of the parts into which E B has been divided. The points F and P will be centres from which the arcs will be described. Join P1 to F1 F2, and P2 to F1 F2 and produce the lines through as shown in figure 2. Now with centre F2 and radius F2 B describe the end arcs, and with centre P and radius P2 C describe the side arcs. If carefully and properly drawn, the arcs should meet and run into each other on the lines drawn through P and F. The object, indeed, for which these lines are drawn is to determine the meeting points of the curves. It should be noticed that the points P may come either within or without the figure, according as the oval is broad or narrow.

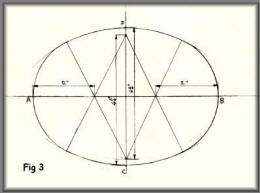
This method is to calculate the required radii. The oval shown is 6 inches by 4½ inches.
The radius for the sides equal 8 times the long diameter minus 5 times the short diameter and divide the remainder by 6.

This equals (8AB – 5CD) ÷ 6 = (48 - 22½) ÷ 6 = 4¼"

The radius for the ends equals 4 times the short diameter minus the large diameter and divide by 6.

This equals (4CD – AB) ÷ 6 = (18 – 6) ÷ 6 = 2"

Lines may be drawn as in sketch 2 to give the exact point of contact of the curves, but with care in drawing any slight discrepancy can be put right using a French curve.

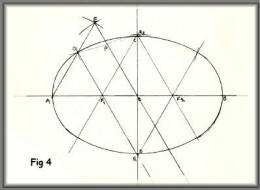
Draw the major and minor axes, intersecting at O. On one half the major axis draw an equilateral triangle OEA on OE mark off OP equal to OC. From C draw through P to find point Q. Then from Q draw QR parallel to OP. With centre R draw CQ. F¹ is the centre of the arc QA. For the opposite arcs, make OF² equal to OF and BP equal to AF².

A word about triangles.

An equilateral triangle, 3 sides of equal length and three angles of 60 degrees.

An isosceles triangle has 2 sides of equal length.

A scalene triangle has three sides all of different lengths.

This is a simple method of drawing an egg shaped oval, but with the drawback that whatever the size of the oval, the ratio of the long axis to the short axis will always be the same (because radius OB will always be twice radius OA).

First, draw the circle ABCD.

With centre D and radius DB draw arc DF.

Draw lines BF through C and DE also through C.

Now with centre C draw arc EF.

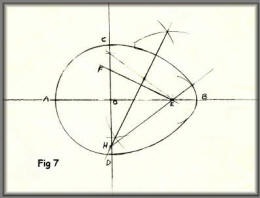
This is a relatively simple method of constructing an egg-shaped oval to choose the length and also the small end radius.

First, draw the major and minor axes AB and CD intersecting at O. Now draw the semicircle for the large end then B to be at the small end, length OB to suit your requirements. Now mark point E so that EB will be the small end radius that you require. Mark point F on the minor axes so that FC = EB, then draw a perpendicular bisector FF to cut OD at H. (H could be outside the oval depending on what dimensions you have chosen - simply extend OH to suit). Now with centre H draw Arc CG, and E is the centre for arc GB.

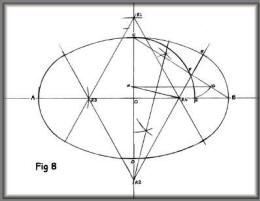
When the major axis is considerably longer than the minor axis, say 4 to 1, all the foregoing methods are not so satisfactory, but for general purposes this method, though not as simple, is workable for all proportions long or broad.

Draw the major and minor axis AB and CD, intersecting at O. Join CB. With centre O and radius OC, draw arc CE, cutting line CB at F. With centre F and radius FE draw arc EG. Draw GH parallel to OB. With compass point on B, make BR4 equal to CH. Join HR4. Bisect HR4 and extend the perpendicular bisector down to meet CD extended at R2. Then R2 is the centre for the side arc and R4 is the centre for the end arc. Make OR3 equal to OR4 to give the centre for the opposite end arc.

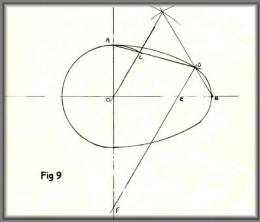
A variation on figure 7 above.

This variation is a little more extended than the ones shown in figure 7.

The method of construction is the same however.

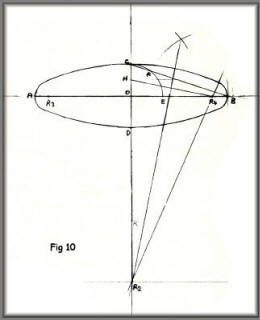
A variation on figure 8 above.

The variation you see in this diagram is that the oval is considerably more flattened than the one seen in figure 8.

You can vary the shape and outline to fit in with your own design by following the guidelines given in the text next to figure 8.

The design methods shown above will give you accurately defined shapes as seen in the ten examples I've included here. You can scale the designs quite easily to fit in with your needs.

Do have a go yourself, you will find it's much easier than you think to draw accurate ovals.